在1月2日到1月4日,学院开展冬季短学期授课,外教Kate老师在这三天带领着我们初步学习了Stata软件,认识并了解了Stata的基础知识,同时以我国GDP和利率数据为例,详细讲解了数据描述及回归方程。
首先我们将数据导入Stata,而原始数据表达时间序列的变量均为字符串类型,为了之后代码运行方便,我们将其中一列转为long类型,代码如下:
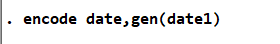
图 1更改类型
输入完成后在右侧变量窗口可以看见一列新的数据。
图 2更改类型结果
数据编辑器中也会出现一列新的蓝色数据。
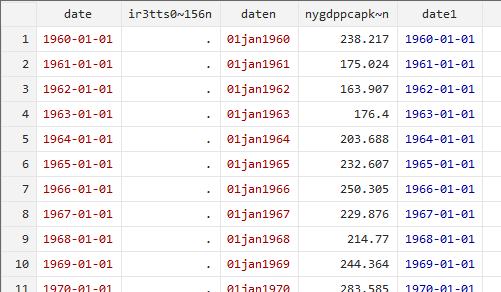
图 3更改类型结果2
将数据初步处理完成之后,我们要简单分析一下数据的结构和趋势,在这时,图表能帮助我们很好地完成这一任务。
散点图和折线图可以帮助我们了解数据大致的趋势。我们可以通过Stata功能栏里的图形制作二维图。

图 4功能栏制作图表
选择散点图,将所要分析的Y变量和X变量分别选中即可得到所对应的散点图。
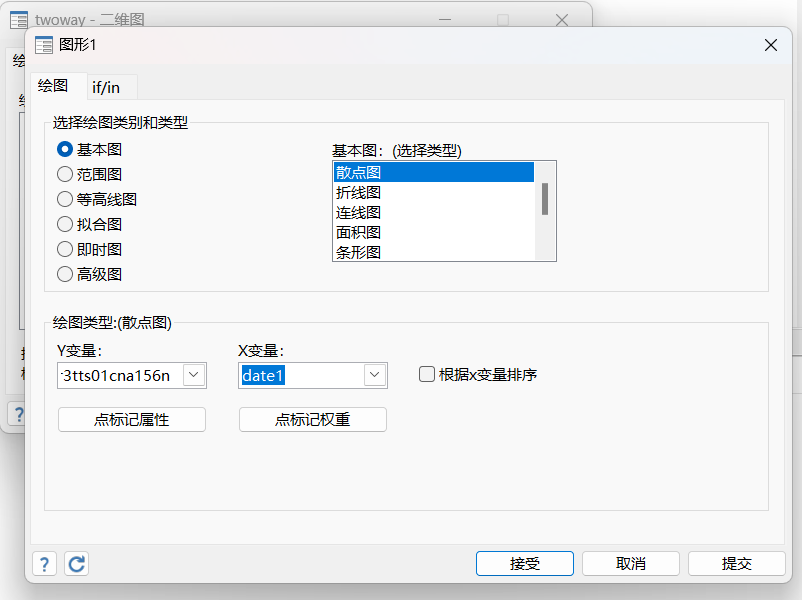
图 5制作图表
我们学习Stata,代码是不可缺少的一部分,因此运用如下代码即可直接生成散点图。
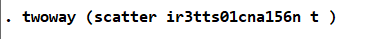
图 6利率散点图代码
输出如下图像:
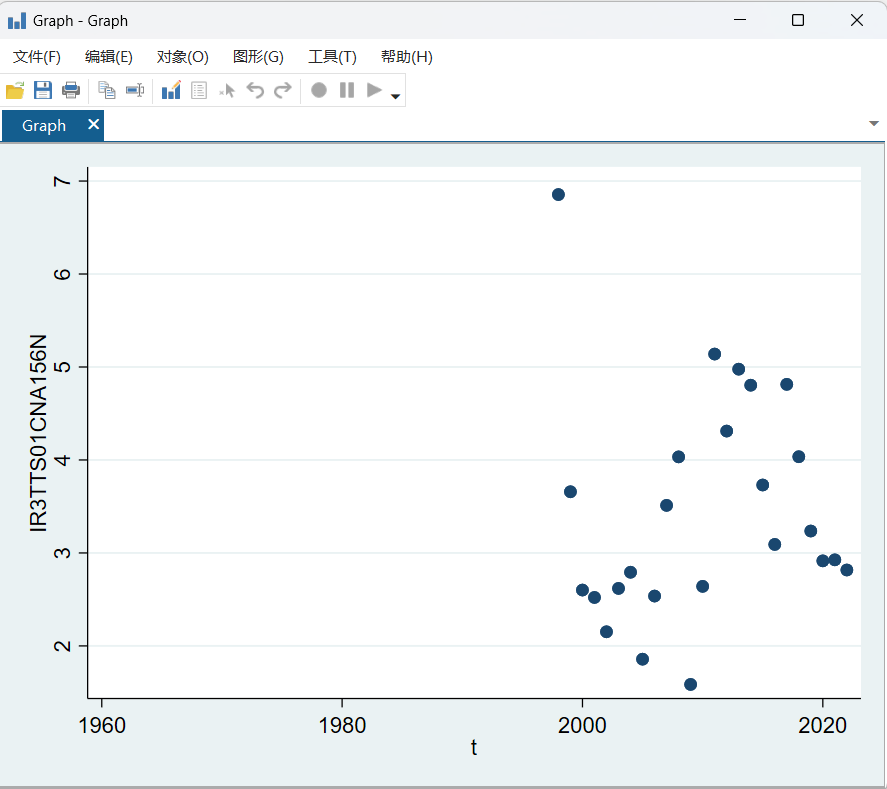
图 7利率散点图
这是将利率作为Y变量,时间作为X变量所得出的结果,我们可以看到由于数据只从1998年开始,因此在1998年以前出现了一大片空白。而之后的数据,分布比较零散,并没有能从中获得更多有用的信息。
运行如下代码,得到新的散点图。
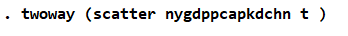
图 8GDP散点图代码
生成结果如下:
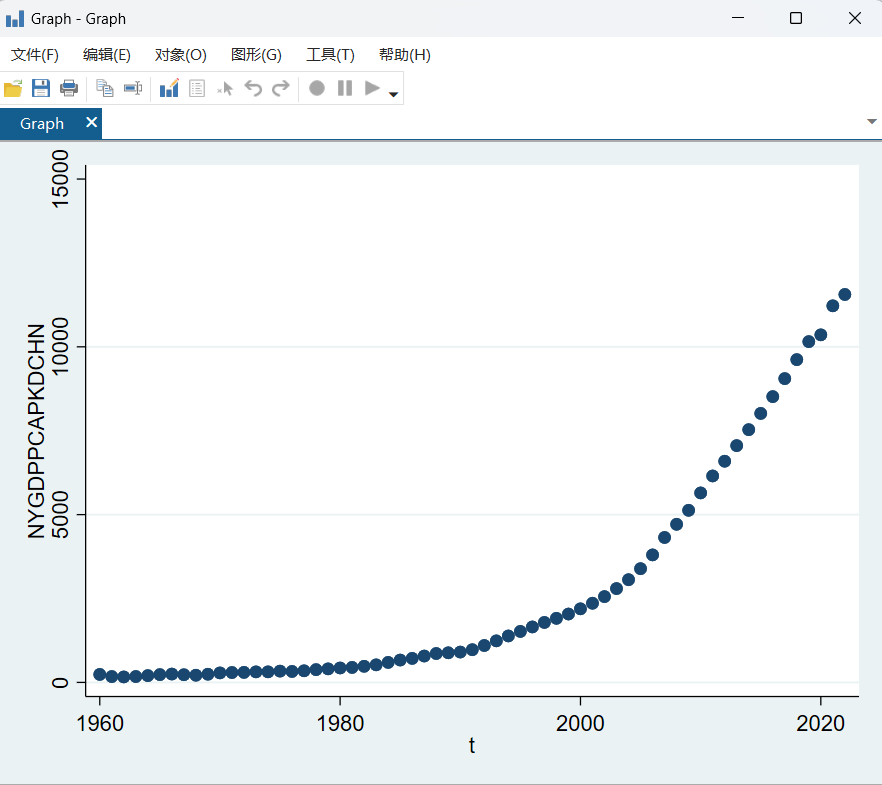
图 9GDP散点图
这是将GDP作为Y变量,时间作为X变量所得出的结果,我们可以看到GDP呈现逐年递增的状态,可以反映出我国发展状况良好。
通过以下代码,可以绘出对应的正态分布图。

图 10利率正态分布代码
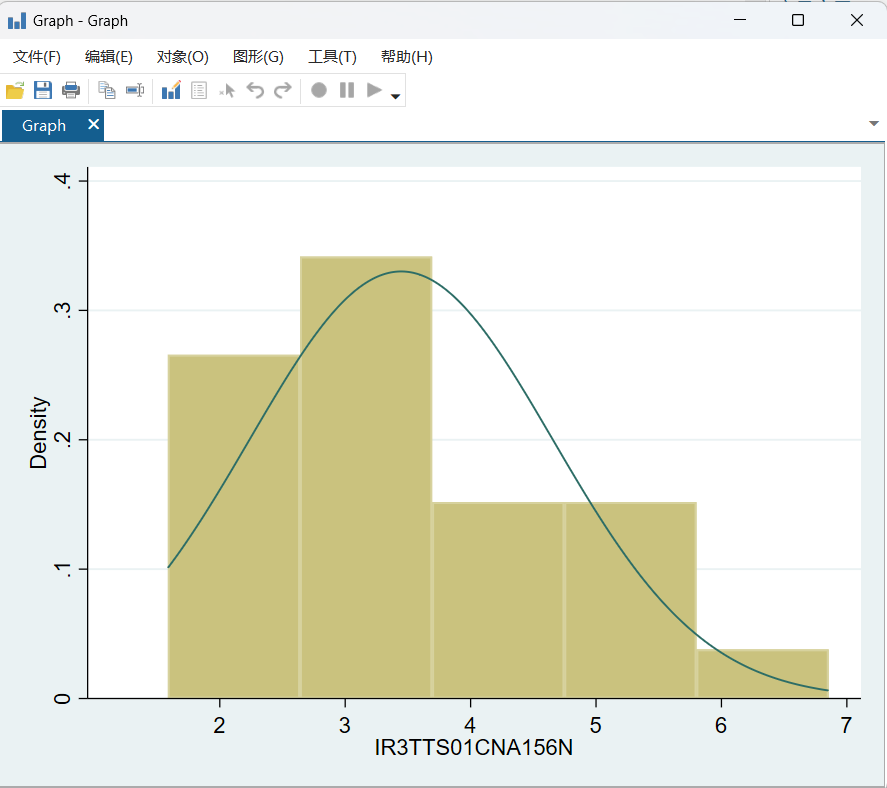
图 11利率正态分布图
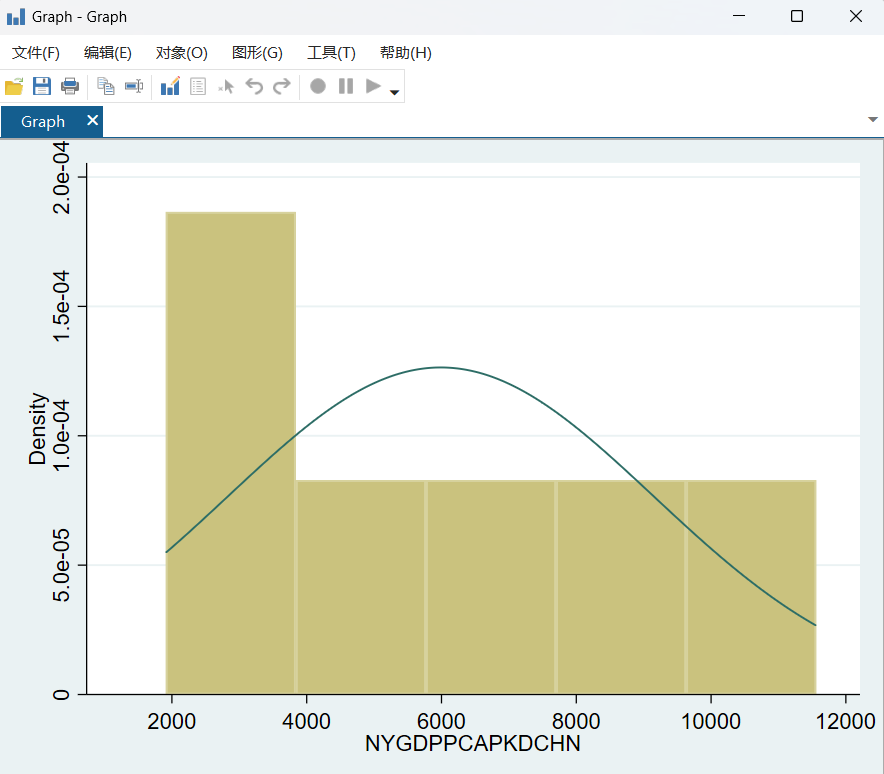
图 12GDP正态分布图
按照同样的方法,我们可以绘出对应的箱线图。
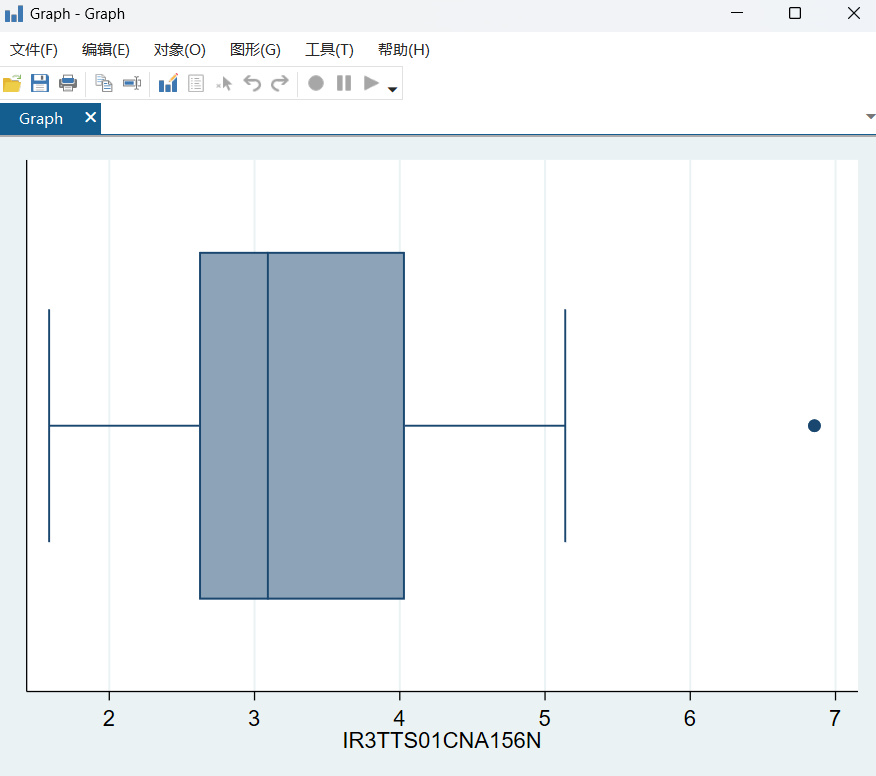
图 13利率箱线图
可以看出利率大多在2.5%到4%之间,说明政策没有很明显的波动,除了1998,就是最后那个点。
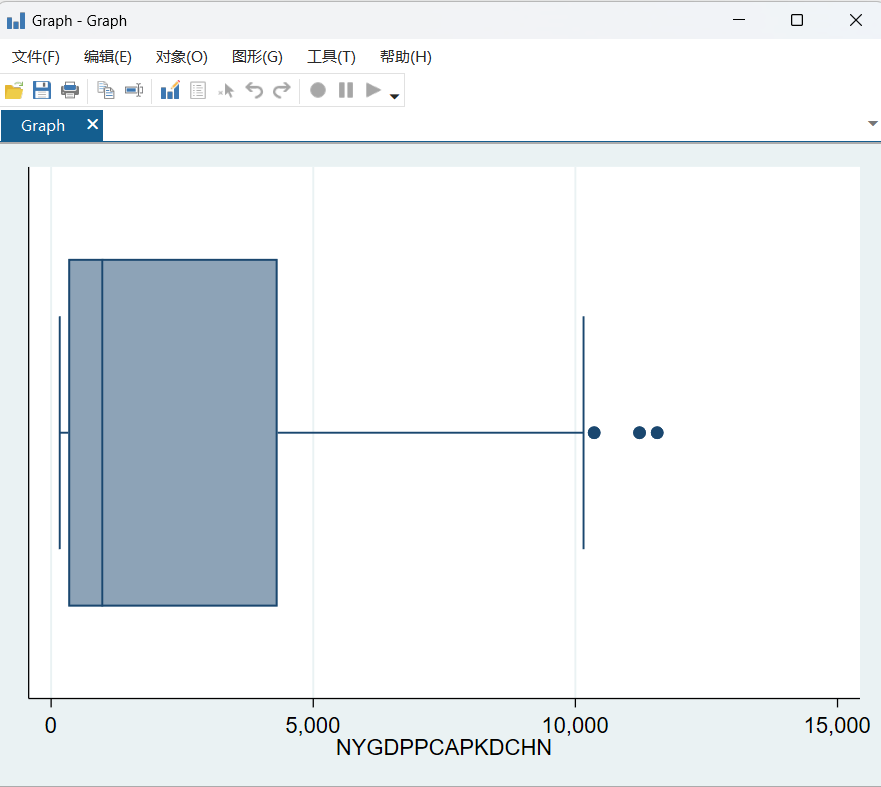
图 14GDP箱线图
这张图所采用的数据是1960年到2022年,前面GDP的散点图前后差距过大,这就导致所生成的这张图对于近期的GDP分析不能有很直观的展现。
接下来是描述性统计,代码如下:
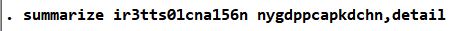
图 15描述性统计代码
生成结果如下:
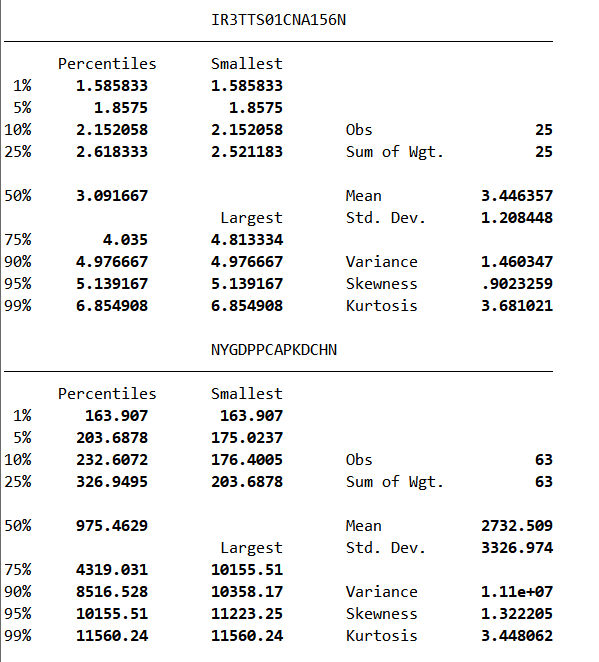
图 16描述性统计1
表的下端的Obs为63,说明GDP统计了63个变量,但表的上端的利率Obs只有25,说明只有25个变量,为了后续数据能够更加精确,我们将GDP前面数据删除,仅留下后25个数据。
新的生成结果如下:
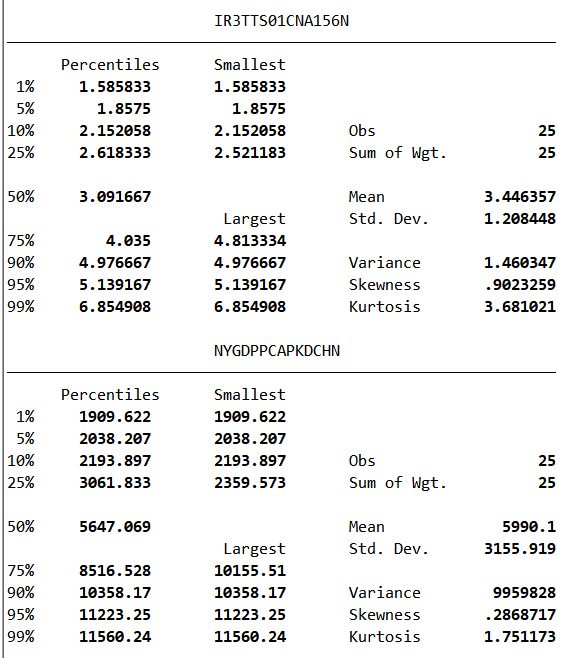
图 17描述性统计2
由上图我们可以得出结论:利率最小值为1.58%,最大值为6.85%,平均值为3.44%,中位数为3.09%;GDP最小值为1909.622,最大值为11560.24,平均值为5990.1,中位数为5647.069。
在正式进行回归分析之前,我们要对该时间序列数据进行时间序列的平稳性检验,如果时间序列非平稳的,那么这个模型的可信度就有所下降并且要修正模型,代码如下:

图 18利率时间序列平稳性检验代码
生成结果如下:
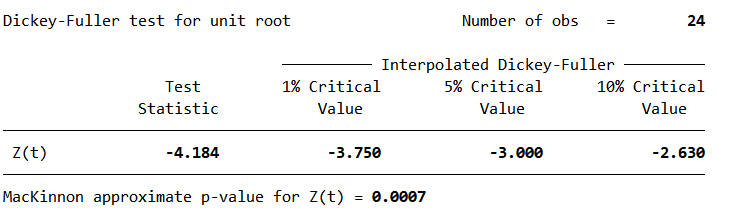
图 19利率时间序列平稳性检验
得出Z(t)=0.0007,因此我们可以拒绝原假设,说明利率是平稳时间序列
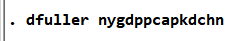
图 20GDP时间序列平稳性检验代码

图 21GDP时间序列平稳性检验
然而,GDP的时间序列是非平稳的,因此我们需要采取其他措施来让它变平稳,生成一列ln函数结果来代替原GDP数据。

图 22生成GDP对数

图 23ln_GDP时间序列平稳性检验
再次进行平稳性检验,得出Z(t)=0.0259,拒绝原假设,说明GDP的对数是平稳的时间序列。
之后通过同样的方法生成ln_i,代码如下:
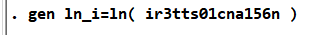
图 24生成ln_i
再对ln_GDP和ln_i进行回归分析,代码如下:
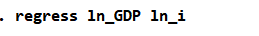
图 25回归分析
生成结果如下:
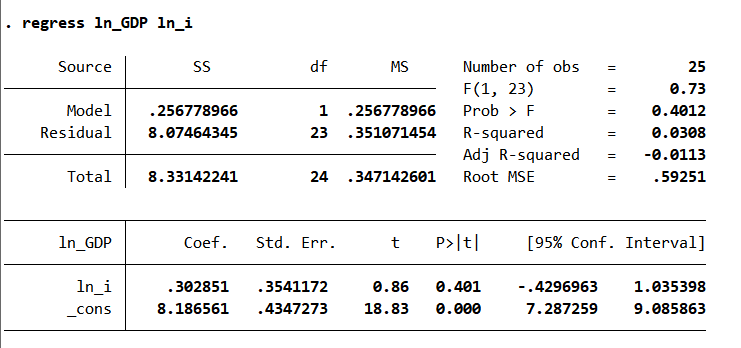
图 26回归结果
根据上图,我们能得到一个回归方程式:。,意味着模型只能解释GDP增长的0.03,所以这次的回归可以说是失败的。将该回归结果绘出图形也可以看到点非常分散。
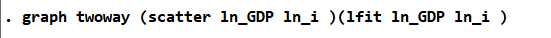
图 27回归图代码
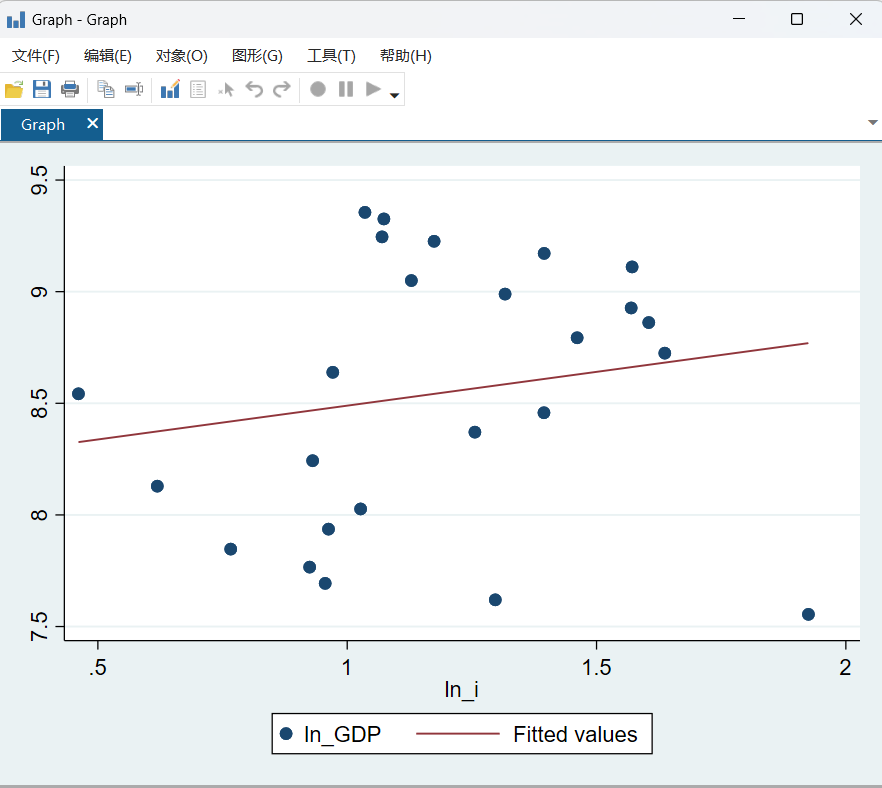
图 28回归图1
既然回归结果并不理想,那么我们可以预测预测变量的值,然后与真实变量进行比较,如果均值相等,那么也可以进行线性回归。代码如下:

图 29预测变量

图 30真实变量与预测变量比较

图 31预测值的正态分布代码
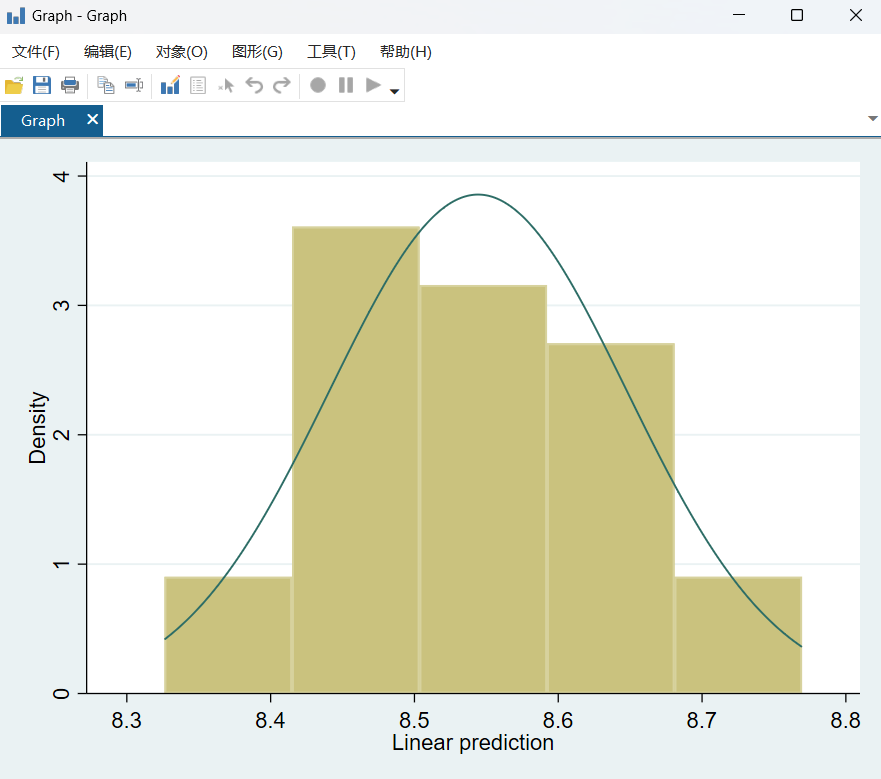
图 32预测值正态分布图
经过对比,两者的均值相等。修正后再进行回归,代码如下:
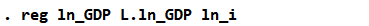
图 33修正后回归代码
生成结果如下:
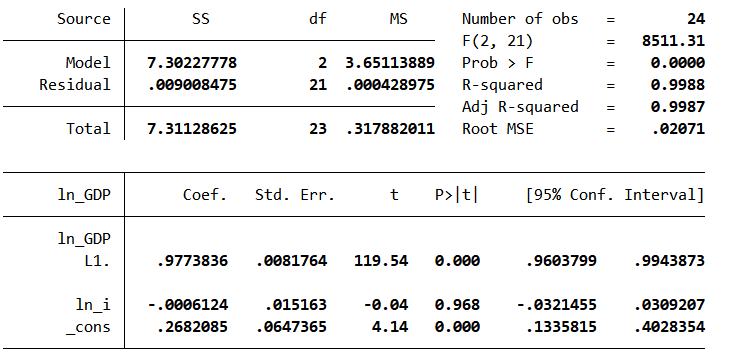
图 34修正后回归结果
得出的回归公式为:,2021年人均GDP增长1%2022年增长97.7%。,比之前的更好。
图 35回归代码2
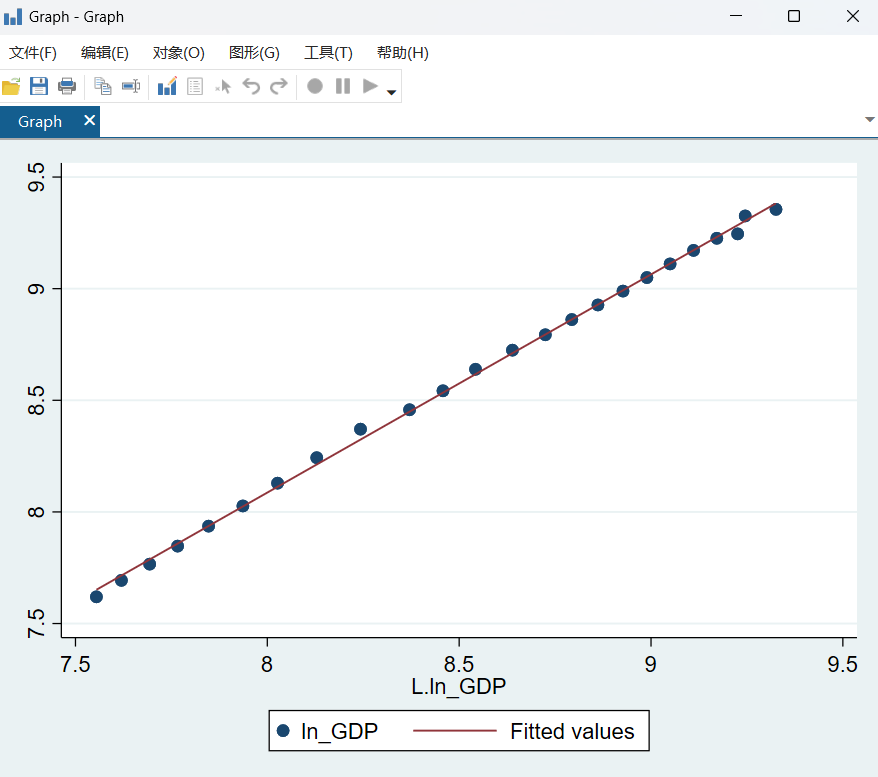
图 36回归图2
以上,就是我在冬季短学期中学到的知识和技能,感受是,熟能生巧,最重的是,模型的解释力来源于研究者对经济事实的理解和领悟。





